integrantes
Oscar Padilla
fernando mejia
pedro zuñiga
VOLÚMENES DE PRISMAS Y PIRÁMIDES
El volumen es una magnitud escala definida como la extensión en tres dimensiones de una región del espacio. Es una magnitud derivada de la longitud, ya que se halla multiplicando la longitud, la anchura y la altura. Desde un punto de vista físico, los cuerpos materiales ocupan un volumen por el hecho de ser extensos, fenómeno que se debe al principio de exclusión de Paulo.
La capacidad y el volumen son términos equivalentes, pero no iguales. Se define la capacidad de un recipiente como la "propiedad de una cosa de contener otras dentro de ciertos límites . La capacidad se refiere al volumen de espacio vacío de alguna cosa que es suficiente para contener a otra u otras cosas.
La unidad medica de volumen en el sistema internacional de unidades es el metro cubico. Para medir la capacidad se utiliza el litro. Por razones históricas, existen unidades separadas para ambas, sin embargo están relacionadas por la equivalencia entre el litro y el decímetro cubico
ejemplos de problemas
Calcula el volumen de un prisma con base rectangular, la cuál tiene de base 8cm y de altura 5cm. Sabemos que h=15 cm
Dibujo

Fórmula Sustitución y Desarrollo Resultado
V= Ab · h A = (8cm) (5cm) A = 40 cm2
A = b · a V = (40 cm2) (10 cm) V = 400 cm3
Partimos del hecho de que el volumen se determina multiplicando el área por la altura del prisma, razón por la cual primero calculo el área de la base del prisma y posteriormente calculo el volumen sustituyendo el valor que obtuve del área multiplicado por la altura.
Ejemplo 2Determina el volumen de una pirámide con base cuadrangular si cada lado mide 5.3 cm y la altura de la pirámide es de 12 cm.
Dibujo

Fórmula Sustitución y Desarrollo Resultado

A = (5.3 cm) (5.3 cm) A = 28.09 cm2
A = l · l V = (28.09 cm2) (12 cm) / 3 V=
337.08 cm3
1.- Determina el volumen de un prisma con una altura de 20 cm. Su base es un octágono regular con lados igual a 6.5 cm y un apotema de 6 cm.
2.- ¿Cuál es el volumen de una pirámide con base triangular de lados igual a 9.5 cm y una altura de 9 cm?. La altura de la pirámide es 16.4 cm
3.- ¿Cuál será la altura de un prisma que tiene un área de 830 cm2 y un volumen de 2400 cm3?
4.- Sabemos que una pirámide tiene una altura de 24.8 cm. y un volumen de 5400 cm3 y ¿A cuánto equivale el área de la base?
5.- ¿A cuánto equivale la altura de una pirámide si sabemos que tiene una área de 978.6 cm2 y un volumen de 9620 cm3?
formulas
Figura
Esquema
Área
Volumen
Cilindro
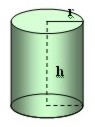
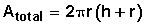
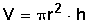
Esfera
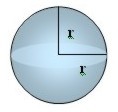
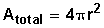
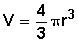
Cono
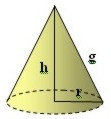

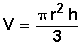
Cubo
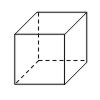
A = 6 a2
V = a3
Prisma
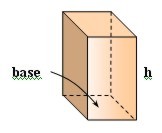
A = (perim. base • h) + 2 • area base
V = área base • h
Pirámide
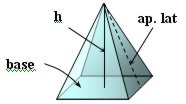
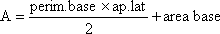

Poliedros regulares
Figura
Esquema
Nº de caras
Área
Tetraedro
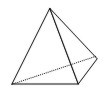
4 caras, triángulos equiláteros 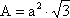
Octaedro
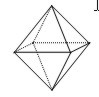
8 caras, triángulos equiláteros 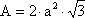
Cubo

6 caras, cuadrados A = 6 a2 Dodecaedro
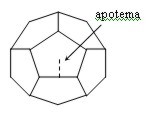
12 caras, pentágonos regulares A = 30 · a · ap. Icosaedro
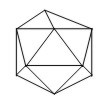
20 caras, triángulos equiláteros 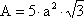
Figura
|
Esquema
|
Área
|
Volumen
|
| Cilindro |  | ||
| Esfera |  | ||
| Cono |  | ||
| Cubo |  |
A = 6 a2
|
V = a3
|
| Prisma |  |
A = (perim. base • h) + 2 • area base
|
V = área base • h
|
| Pirámide |  |
Poliedros regulares
Figura
|
Esquema
|
Nº de caras
|
Área
|
| Tetraedro |  | 4 caras, triángulos equiláteros | |
| Octaedro |  | 8 caras, triángulos equiláteros | |
| Cubo |  | 6 caras, cuadrados | A = 6 a2 |
| Dodecaedro |  | 12 caras, pentágonos regulares | A = 30 · a · ap. |
| Icosaedro |  | 20 caras, triángulos equiláteros |